Primeiro vamos separar em dois triângulos como manda a figura. Para visualizar melhor vamos separar o triangulo BAD em azul e CDB em verde.

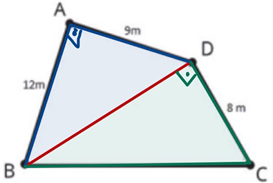
Para ficar ainda mais visível vamos separar ainda mais estes triângulos. Desta forma temos:

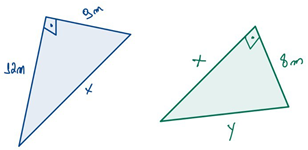
Como queremos calcular a área e o perímetro precisamos lembrar que:

Área = (Base x Altura)/2

Perímetro = Soma de todos os lados

Logo precisamos calcular os valores de x e y para que possamos usar nas formulas.

Pelo retângulo azul podemos utilizar o teorema de Pitágoras (H² = a² + b²) para achar o valor de x. Basta repararmos que x é oposto ao sinal de ângulo retângulo, portanto x é a hipotenusa do retângulo azul:

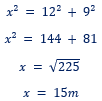
Para y temos um caso similar ao anterior, onde o valor de x, que agora sabemos que vale 15m, e y, agora no triângulo verde, equivale a hipotenusa do triângulo verde. Portanto temos:

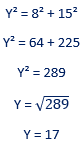
Agora que sabemos o valor de x e y, podemos calcular as áreas das figuras.

Para a figura azul temos que a base e altura são os lados diferente da hipotenusa, ou seja:

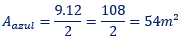
Para a área verde temos a mesma interpretação:

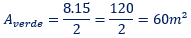
podemos calcular a área total da figura:

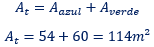
Para o Perímetro da figura temos que considerar que na figura inicial a parte de baixo, que antes falta o valor, agora corresponde ao valor de Y:

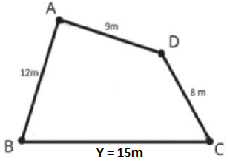
Portanto:

P = 12 + 9 + 8 + 17

P = 46m

Portanto, a área corresponde a 114m² e o perímetro a 46m.

Resposta: A